The pump operating point pumps is discussed in the page pumps, we see here an example of calculation of the operating point of the pump, This is similar to ventilations or apiration (with no control of NPSH because no risk of cavitation with the air).

The flow rate that delivers a centrifugal pump or fan decreases depending on the pressure resistant (load height or Delta pressure) of the fluid's network. This resistance of the network is the pressure that must provide the pump or fan, to achieve a given rate.

the manufacturer provides with the pump, a flow curve of evolution, as a function of the pressure resistant, that the pump has to overcome.. The curves are generally provided for a family of pump. Pressure (or delta P for the fans), is given in Hm (manometric head) for liquids, or Pascals for aeraulic.

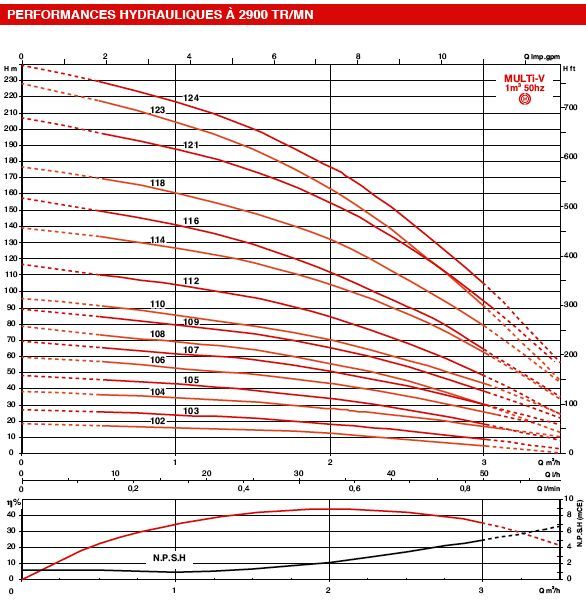
point fonctionnement courbe pompes

  • As a simple reminder, 1 meter water column produces a pressure (Density X Gravity X Height) 1000 x 9,81 x 1 = 9810 pascals. 1 bar=100 000 pascals we note that 1 bar = 10 water meters = 100 000 pascals
This curve shows the characteristics of a series of pump. A series of pump, is constituted by the same pump of which only the wheel diameter was reduced.

Pump wheel diameter reduced: In theory the flow and manometric head are proportional to the square of the diameter of the wheel. wheel diameter reduced is used to modify the pump flow without modifying its performance, (in a limit of 15% of the initial diameter), This therefore gives the possibility to manufacturer, to using a model of pump to produce a range of pumps perfectly adapted to various specifications.

We see for example that the pump with wheel 116 mm provides a pressure of 110 Meters, to flow rate of 2 m3 /h in its area of ​​best efficiency (about 42% ). Here we can read the graph of the pump, It remains to see if it corresponds to our network. The question that arises is: What is the pressure required to circulate the fluid in our system, to the flow rate that we want to achieve? At the flow rate that we want to achieve, the pressure provided by the pump must be equal to the sum of: If the network is open:
  • static pressure: Height difference between the point of input and output circuit (zero if the network is closed. See hydrostatic head)
  • Dynamic pressure: acceleration of the fluid, it is the kinetic-energy (speed) supplied to the fluid.
If the network is closed, the energy expended to climb the height difference is returned in descending parts, Thus the difference in height (static pressure) does not come into account, If the network is closed, the fluid velocity at the output is returned as input, therefore the Dynamic pressure is not taken into account.
  • The operating point of the system "pump / network" is the flow rate that balances the pressure supplied by the pump and pressure necessary for the operation of the network flow.
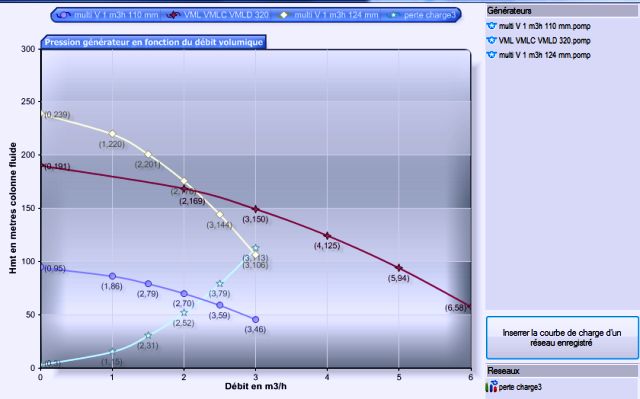
The resolution of this problem, is done by interpolating curve network load, and the load curve of the pump: Here we see three pump curves, compared to a network pressure drop curve (light blue) It is easy to see the operating points for these three pumps:

pump curves, compared to a network pressure

  • The yellow curve intersects the curve network, to operating point 3 m³/h
  • The dark blue curve intersects the curve network, to operating point 2,2 m³/h
  • The red curve pump is outside the range of flow in which the network was tested (light blue curve) But we can imagine that if the curve network continues to evolve in this way, it crosses the red line at the operating point of 3,5 m³/h

Another example video: