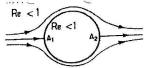
 Re<1: At low speeds, the current lines are symmetrical. Two points stopping are observed A1 et A2. It is creeping flow regime.
Re<1: At low speeds, the current lines are symmetrical. Two points stopping are observed A1 et A2. It is creeping flow regime.
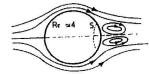 Re=4: If Re increases, the detachment appears to the rear of the sphere along a circle S in conjunction with a vortex-ring centered on the axis of the sphere.
Re=4: If Re increases, the detachment appears to the rear of the sphere along a circle S in conjunction with a vortex-ring centered on the axis of the sphere.
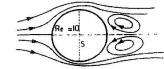 Re=10 Increasing Re, the vortex increases in volume to fill all the back of the sphere and the circle of detachment S is substantially diametrical.
Re=10 Increasing Re, the vortex increases in volume to fill all the back of the sphere and the circle of detachment S is substantially diametrical.
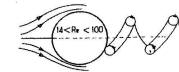 Re=14,
Re=14,
the swirl Detaches and takes a helical shape while the sphere is subjected to a transverse force revolving around u, the flow regime is not continuous but continuous on average.
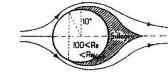 Re=100,it appears a circle of detachment at 10° on the front of the sphere. Behind The wake is an area where the speed varies statistically around a mean value of zero.
Re=100,it appears a circle of detachment at 10° on the front of the sphere. Behind The wake is an area where the speed varies statistically around a mean value of zero.
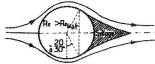 Re =(1Oe5 à 10e6), The circle of detachment suddenly shifts back and the wake is reduced.
Re =(1Oe5 à 10e6), The circle of detachment suddenly shifts back and the wake is reduced.
It is assumed that :
-
at Re<(1Oe5 à 10e6), the separation occurs in the Laminar Boundary Layer.
-
at Re>(1Oe5 à 10e6), the separation occurs in the turbulent Boundary Layer.
-
atr Re =(1Oe5 à 10e6),
there is detachment at the transition point of the boundary layer. . The value of Re depends greatly on the state of the surface of the sphere .The value of "Re sudden movement of the circle of detachment" is lowered by increasing the roughness of the sphere, This precipitates the onset of turbulent boundary layer.
Variation coefficient of drag (cd) of a sphere (line) and a disk (dotted line) as a function of the Reynolds number
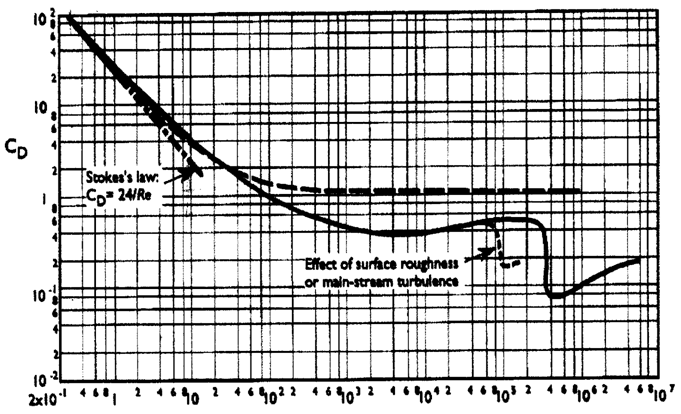
Variation coefficient of drag of a cylinder of "endless length" perpendicular to the fluid stream, as a function of the Reynolds number:
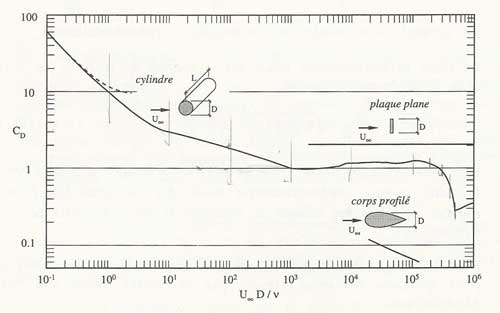
see: Reynolds , hydrodynamique
With MECAFLUX standard
Enter the diameter and roughness of your area, choose the fluid, enter the flow velocity, and Cd and the drag force in Newton, will be given depending on the Reynolds number
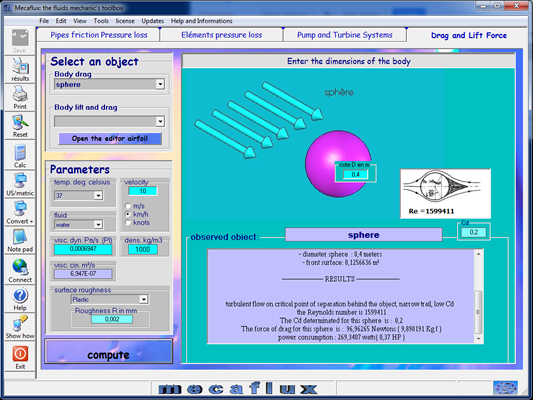
Mecaflux integrates (in the drag and lift tab), the calculation of the drag of spheres and perpendicular cylinder of given length by applying a correction function of the length / diameter ratio of the cylinder. The angle can also be parametered (90/60/30/0):