-
Acceleration unit
Unité de l'accélération: mètres secondes par secondes(m/s²)
For an object to stop, taking a speed of 1 meters per second per second,At the end of the second second, the object will have a speed of (1m/s x 2) =2 m/s
-
Acceleration calculation
Newton's second law:Force=mass x acceleration
A force (F) in Newtons applied to an object mass (m) Kg causes an acceleration (a) in m / s ² of that object as F / m = a
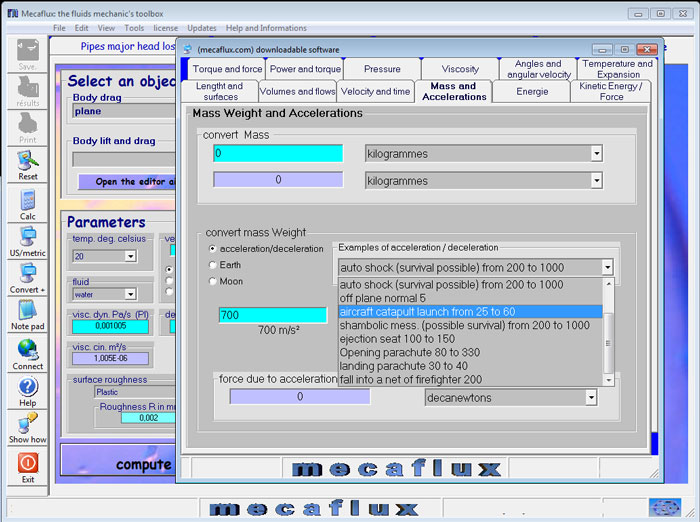
This equation is implemented with a few representative examples of acceleration and deceleration (accident, elevator..),in the mass and acceleration tab of the converter included in mecaflux.
Based on the assumption :"any force acting alone is proportional to the acceleration" and considering that " the weight of an object (the force applied thereto) is the force, gravity is determined as the acceleration of the mass of an object , which gives the weight of the object
on earth this acceleration is 9.81m/s² at poles and 9.78m/s² at the equator (effect ofthe centrifugal force)
on the moon that acceleration is 1.62m/s²
Representative examples of the effects of gravity (accident, elevator..),in the mass and acceleration tab of the converter included in mecaflux.
-
centripetal acceleration
Consider an object whose path is a curve, the force which tends to move away the object from the center is the centrifugal force
a force that keeps the object near the center is the centripetal force
These two forces are equal and opposite because they are action and reaction. One does not exist without the other
With m=mass of the object, R=the radius of the circular path of the object, a= centripetal acceleration, and V=speed of the object :
m V²/R= Force
a=V²/R
-
Acceleration of fluid
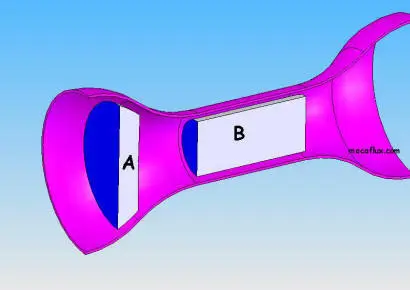
In a narrowing tube, the acceleration of the fluid is related to a pressure loss. This is the Bernoulli effect or Venturi effect
If the tube narrows between point A and point B :
The continuity equation gives us a speed increase, due to the narrowing of the section as:
(Section A)x(Velocity A)=(Section B)x(Velocity B)=Constant volumetric flow, we deduce the velocity at B
(Velocity B)=(Section A)/(Section B)x(Velocity A)
Bernoulli's equation links the pressure and the speed:(we assume the horizontal tube, not to take account of changes in height).
(pressure at point A)+(1/2 density) x (velocity point A)²=(pressure at point B)+(1/2 density) x (velocity point B)²
substituting (velocity point B) by [(Section A)/(Section B)x(Velocity A)] we get:
(pressure A)+(1/2 density )x( velocity A)²=(pressure B)+(1/2density)x([(Section A)/(Section B)x(Vitesse A)])²
if we know the pressure drop and the sections of the tubes we can deduce the velocity at A:
pressure drop=(pressure A)-(pressure B)=1/2density x(velocity A)² x[(Section A²)/(Section B²)-1]
Knowing the speed of A we can deduce the speed at B by the continuity equation mentioned above.
if we know the speed and the sections of the tubes we can deduce the pressure drop..
The applications of these equations: Flow Venturi water jet vacuum systems using compressed air stream, spray ...
Mecaflux standard comes with a converter, with functions related to acceleration..
mass acceleration deceleration relationship weight / shock in the converter :
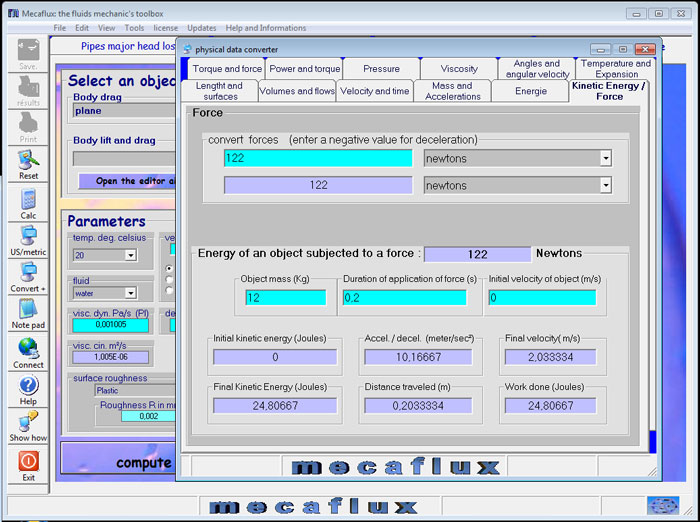
relation kinetic energy acceleration in the converter